Số phức luôn là phần kiến thức khó trong chương trình đại số lớp toán 12. Vậy số phức là gì có các dạng bài tập nào và làm thế nào để ăn chắc điểm dạng bài tập này? Các em hãy theo dõi bài viết dưới đây để được tổng hợp đầy đủ cả lý thuyết cũng như cách giải bài tập số phức đạt điểm tối đa trong kỳ thi THPT Quốc Gia sắp tới nhé!
1. Số phức là gì?
Số phức là số được viết dưới dạng a + bi trong đó a, b là số thực và $i^{2} = -1$, trong đó a và b là các số thức i là đơn vị ảo, $i^{2} = -1$ hay $i^{2}= \sqrt{-1}$. Trong biểu thức này, số a gọi là phần thực, b gọi là phần ảo của số phức.
Ngoài ra, số phức còn có thể biểu diễn trên mặt phẳng phức với trục hoành là trục số thực và trục tung chính là trục số ảo. Do đó một số phức a+ bi được xác định bằng một điểm có tọa độ (a,b). Theo đó một số phức nếu có phần thực bằng 0 thì gọi là số thuần ảo (hay số ảo), nếu có phần ảo bằng không thì trở thành số thực R.
2. Ứng dụng của số phức
Khi các em học kiến thức về phần số phức sẽ thấy kiến thức này được ứng dụng để giải nhiều dạng bài tập khác mang lại hiệu quả cao trong kỳ thi.
2.1. Số phức trong hình học và lượng giác
Theo như khái niệm về số phức thì i chính là sự quay và chuyển hướng 90 độ nên số phức có một vai trò quan trọng trong việc giải các bài tập hình học phẳng và bài tập lượng giác. Các em chỉ cần áp dụng kiến thức số phức thì hoàn toàn có thể giải được các bài toán hình phẳng cũng như xử lý gọn các công thức lượng giác phức tạp.
Ngoài ra, số phức còn được ứng dụng vào giải các dạng bài tập liên quan khác như: phân tích đa thức ra thừa số, tính toán trong các bài tập về tích phân…
Dưới đây là một số dạng bài tập toán điển hình:
2.2. Số phức trong các môn học khác và trong đời sống
Khi các em học về số phức thì có thể dễ dàng nhận thấy số phức không chỉ được ứng dụng nhiều trong toán học mà còn cả trong vật lý. Các em có thể dễ dàng nhận thấy vật lý có liên quan rất nhiều đến đến hình học và nhiều đại lượng đo hướng mà nói về hướng là phải nói đến số phức. Vì như các em đã biết trong số phức thì phần số ảo i chính là đại diện cho sự quay 90 độ.
Ngoài ra, trong vật lý phần nguyên tử và khái niệm hàm sóng người ta cũng dùng số phức để để mô tả vật chất biến đổi theo thời gian. Việc sử dụng số phức trong vật lý sẽ giúp em biểu diễn thuận lợi hơn so với dùng số thực rất nhiều. Vì vậy, hãy ứng dụng tối đa phần kiến thức này trong quá trình học tập cũng như trong cuộc sống nhé!
Tham khảo ngay bộ tài liệu tổng hợp kiến thức và phương pháp giải mọi dạng bài tập trong đề thi Toán THPT Quốc gia
3. Tổng hợp các khái niệm liên quan đến số phức
Để có thể áp dụng làm các bài tập về số phức thì em cần nắm được các khái niệm liên quan đến số phức như sau:
3.1. Số phức liên hợp
Định nghĩa: Số phức liên hợp có dạng: Z= a+ bi, số phức $\overline{Z}= a+ bi$ được gọi là số phức liên hợp của Z.
Số phức liên hợp có 1 số tính chất như sau:
1. $Z x \overline{Z} = a^{2}+ b^{2}$ là một số thực
2. $Z+ \overline{Z} = 2a$ là một số thực
3. $\overline{Z+Z'} = \overline{Z} + \overline{Z’}$
4. $\overline{Z x Z'} = \overline{Z} x \overline{Z’}$
3.2. Số phức nghịch đảo
Có thể nói, số phức nghịch đảo, hay nghịch đảo của số phức Z (kí hiệu là $Z^{-1}$ là số phức có dạng sao cho tích của số phức nghịch đảo với số phức Z là bằng 1).
Ta có thể chứng minh: $Z^{-1} = \frac{1}{\left | Z^{2} \right |}\overline{Z}$ = $\frac{1}{a^{2}+b^{2}} (a-bi)$
$⇒ Z^{-1}.Z = \frac{1}{\left | Z^{2} \right |} (a-bi)(a+bi)$ = $\frac{a^{2}-b^{2}.i^{2}}{a^{2}+b^{2}}$ = 1
Số phức dạng nghịch đảo của Z = a+bi là số phức $Z^{-1}=\frac{1}{Z}= \frac{1}{a+bi}$
Số nghịch đảo của Z = a+bi # 0 là số $Z^{-1}= \frac{1}{Z} = \frac{\overline{Z}}{\left | Z^{2} \right |}$
3.3. Số phức thuần ảo
Định nghĩa: Số phức thuần ảo là khi phần thực a = 0 thì Z = bi thuộc R. Khi đó Z được gọi là số thuần ảo
3.4. Modun số phức
Modun của số phức Z = a+bi là độ dài của vectơ u(a,b) biểu diễn số phức đó
Theo một định nghĩa khác thì số phức modun Z = a+bi ($a,b\in R$) là căn bậc hai số học của $a^{2}+ b^{2}$.
Ví dụ: 3+ 4i = 25 ⇒ 3+ 4i= 5
Ta dễ dàng nhận thấy trị tuyệt đối của số thực cũng chính là modun của số thực đó. Do đó đôi khi ta cũng có thể gọi modun của số phức là trị tuyệt đối của số phức. Modun số phức có công thức như sau:
$z=a+bi$,$a\in R$,$b\in R \rightarrow \left | z \right |=\sqrt{a^{2}+b^{2}}$
Ký hiệu: $\left | z \right |$=$\sqrt{a^{2}+b^{2}}$
+ $\left | z_{1}z_{2} \right |$=$\left | z_{1} \right |.\left | z_{2} \right |$
+ $\left | \left | z_{1} \right |\left | z_{2} \right | \right |\leq \left | z_{1} \right |+\left | z_{2} \right |$
+ $z_{1}/z_{2}$=$z_{1}\overline{z_{2}}/\left | z_{2} \right |^{2}$
Về mặt hình học, mỗi số phức Z = a+bi ($a,b\in R$) được biểu diễn bởi một điểm M(z)= (a,b) trên mặt phẳng O_{xy} và ngược lại. Khi đó modun của Z được biểu diễn bởi độ dài đoạn thẳng OM(z). Rõ ràng, modun của z là một số thực không âm và nó chỉ bằng 0 khi Z=0.
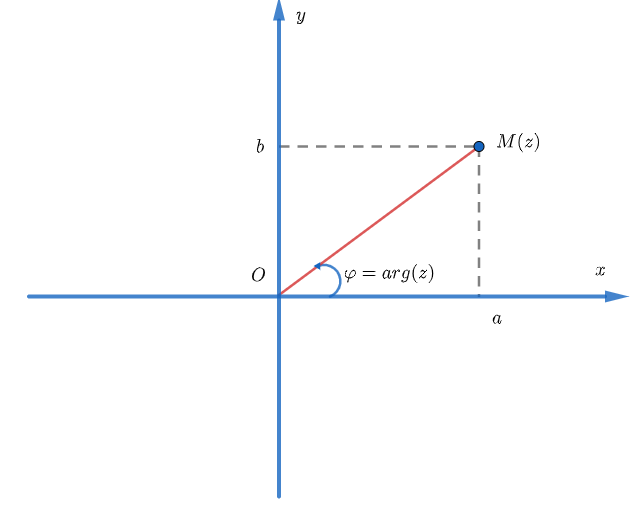
3.5. Argument của số phức
Để hiểu về Argument của số phức giả sử ta có M(z) là điểm biểu diễn số phức z. Arg (z) là góc định hướng giữa chiều dương của trục thực và tia OM(z) thỏa mãn $-n< Arg(z)\leq n$.
Vậy nên rõ ràng nếu $z= a+bi (a,b\in R)$ thì $Arg (z) = Arctan(b/a)$
4. Biểu diễn hình học của số phức
Ta có số phức z= a+bi (a,b nguyên). Khi đó xét mặt phẳng phức Oxy, z được biểu diễn bởi điểm M(a,b) hoặc vectơ u= (a,b). Lưu ý ở mặt phẳng phức, trục Ox được gọi là trục thực, Oy được gọi là trục ảo.
5. Hướng dẫn giải các dạng bài tập số phức cơ bản
5.1. Bài tập dạng tìm số phức w=iz+z
Ví dụ: Tìm số thực x,y sao cho đẳng thức sau là đúng
$5x+y+5xi=2y-1+ (x-y)i$
Giải:
Ta xét mỗi vế là 1 số phức, suy ra điều kiện để 2 số phức bằng nhau là phần thực bằng phần thực, phần ảo bằng phần ảo:
⇒ 5x+y= 2y-1; 5x= x-y ⇒ x= 1/7; y+ 4/7
5.2. Tìm số phức dạng e mũ
Số phức z = a + bi, số phức w = x + yi được gọi là căn bậc hai của z nếu w2 = z, hay nói cách khác:
$(x+y)^{2}$= a + bi
$=> x^{2}-y^{2} + 2xyi$ = a + bi
$=> x^{2}-y^{2} = a$, 2xy=b(*).
Như vậy để tìm căn bậc 2 của một số phức, ta sẽ giải hệ phương trình (*) ở đã nêu ở trên.
Ví dụ: Tìm giá trị của m để phương trình sau z + mz + i = 0 có hai nghiệm $z_{1}$,$z_{2}$ thỏa đẳng thức
$z_{2}^{1} + z_{2}^{2}-(z_{1}z_{2})^{2}-2z_{1}z_{2}$= -4i.
Giải:
Với phương trình bậc 2 hệ thức Vi-ét về nghiệm luôn được sử dụng
Suy ra ta có $z^{1} + z^{2}$ = -m, $z_{1}z_{2}$= i
Theo bài ra ta có:
$z_{2}^{1}+ z_{2}^{2}$= -4i.
$⇒ (z_{1}z_{2})^{2}-2z_{1}z_{2}$=-4i
$⇒ m^{2}$= -2i
Ta quy về tìm căn bậc hai cho 1 số phức. Áp dụng phần kiến thức đã nêu ở trên, ta giải hệ sau: gọi m= a+bi, suy ra ta có hệ:
$a^{2}+b^{2}$=0. 2ab= -2i
⇒ (a,b)= (1,-1) hoặc (a,b)= (-1,1)
Vậy có hai giá trị của m thỏa mãn đề bài.
5.3. Bài tập số phức dạng lượng giác
Để chuyển số phức z = a + bi sang dạng lượng giác z = $r(cos\varphi +isin\varphi )$ ta phải tìm được môđun và argumen của số phức. Bằng việc đồng nhất biểu thức hai số phức ta có:
>> Xem thêm: Tổng hợp các dạng phương trình lượng giác thường gặp
5.4. Phương trình bậc 4 số phức
Sau bài viết này, hy vọng các em đã nắm chắc được toàn bộ lý thuyết và bài tập áp dụng của số phức. Để có thêm nhiều kiến thức hay thì em có thể truy cập ngay Vuihoc.vn để đăng ký tài khoản hoặc liên hệ trung tâm hỗ trợ để có được kiến thức tốt nhất chuẩn bị cho kỳ thi đại học sắp tới nhé!
Tham khảo thêm:
Bộ Sách Thần Tốc Luyện Đề Toán - Lý - Hóa THPT Có Giải Chi Tiết
>> Xem thêm: Tổng ôn tập số phức - full lý thuyết và bài tập
